回溯类题目套路
- 所有答案的集合可以看作成为一棵树
- 第一层节点到树的叶子节点的所有路径即为答案之一
那么回溯的题目就可以转变为求答案树上,第一层节点到叶子节点是所有路径。在寻找所有路径的编码过程中,有如下两个注意点
- 终结条件
- 还原现场
- 去重
- 电话号码的所有组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
假设字符串dig为“23”,构成的树如下
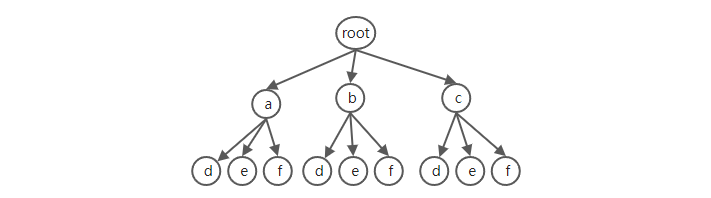
编码时使用StringBuilder作为临时答案stb 终结条件:stb.length == dig.length 还原现场:stb.remove(dig.length) 去重:不涉及
- 复原id地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
- 例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你不能重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
假设字符串为s = "25525511135",构成的树如下
使用List<String>作为临时答案tempList 终结条件:tempList.size() == 4 且s全部用完 还原现场:tempList.remove(tempList.size() - 1),s用掉的还原 去重:不涉及
- 单词搜索 79
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
使用index表示现在已经匹配的字母数 终结条件:index == word.length 下一步的条件:当前位置的上下左右四个方向上,与word[index + 1]相同的数 去重:使用m x n的visited数组,使用过的字母标记为true
- 二叉树的所有路径
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。 叶子节点 是指没有子节点的节点。
终结条件:到达叶子节点
- 全排列 46
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
使用List<Integer> temp 作为临时答案,每次添加nums数组中的某个数 终结条件:temp.size() == nums.length 去重:使用visited数组
- 全排列2 47
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
使用List<Integer> temp 作为临时答案,每次添加nums数组中的某个数 终结条件:temp.size() == nums.length 去重:
使用visited数组
对nums排序,当nums[i] == nums[i - 1]时,有如下两种情况
- visited[i - 1] = true,说明不在树的同一级
- visited[i - 1] = false,说明在树的同一级,即为应该排除的重复情况
组合 77
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。
使用List<Integer> temp作为临时答案,每次添加[1,n]中的一个数 终结条件:temp.size() == k 去重:使用visited数组
- 组合总和 36
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
使用List<Integer> temp作为临时答案,sum作为temp中数值之和,每次添加candidates中的一个数 终结条件:sum == target
- 含有相同元素的组合总和 40
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用一次。
注意:解集不能包含重复的组合。
使用List<Integer> temp作为临时答案,sum作为temp中数值之和,每次添加candidates中的一个数 终结条件:sum == target 去重:
visited数组
将candidates排序,当candidates[i] == candidates[i - 1] && !visited[i - 1]
数组总和3 216
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。 说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
使用List<Integer> temp作为临时答案,sum作为temp中数值之和,每次添加[1,9]中的一个数 终结条件:temp.size() = k 去重:
visited数组
将candidates排序,当candidates[i] == candidates[i - 1] && !visited[i - 1]
子集 78
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
使用List<Integer> temp作为临时答案,每次添加nums中的一个数 去重:使用index表示当前取到nums数组的位置,每次只能取nums中下标在index之后数
- 子集2 90
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
使用List<Integer> temp作为临时答案,每次添加nums中的一个数 去重:
使用visited数组
将nums排序,当nums[i] == nums[i - 1] && !visited[i - 1]
分割字符串 131
给你一个字符串 s,请你将_ s _分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。 回文串 是正着读和反着读都一样的字符串
使用List<String>temp 作为临时答案,每次添加s中的一个回文子串st,并将s-st作为s重复此步骤 终结情况:s-st为空
- 数独 37
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分空格内已填入了数字,空白格用 '.' 表示。
将所有未填入的空格信息入栈stack,对每个栈中的数,对其能取的数依次尝试
如位置(0, 2) x轴:5、3、7 y轴:8 第一象限:3、5、6、8、9 故位置(0,2)只能选1、2、4
终结情况:stack为空
- n皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。 给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。 每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
将第n个皇后放在第n层,对第n层的每个位置进行尝试,若第n个皇后也有位置则为解法之一



