排序算法
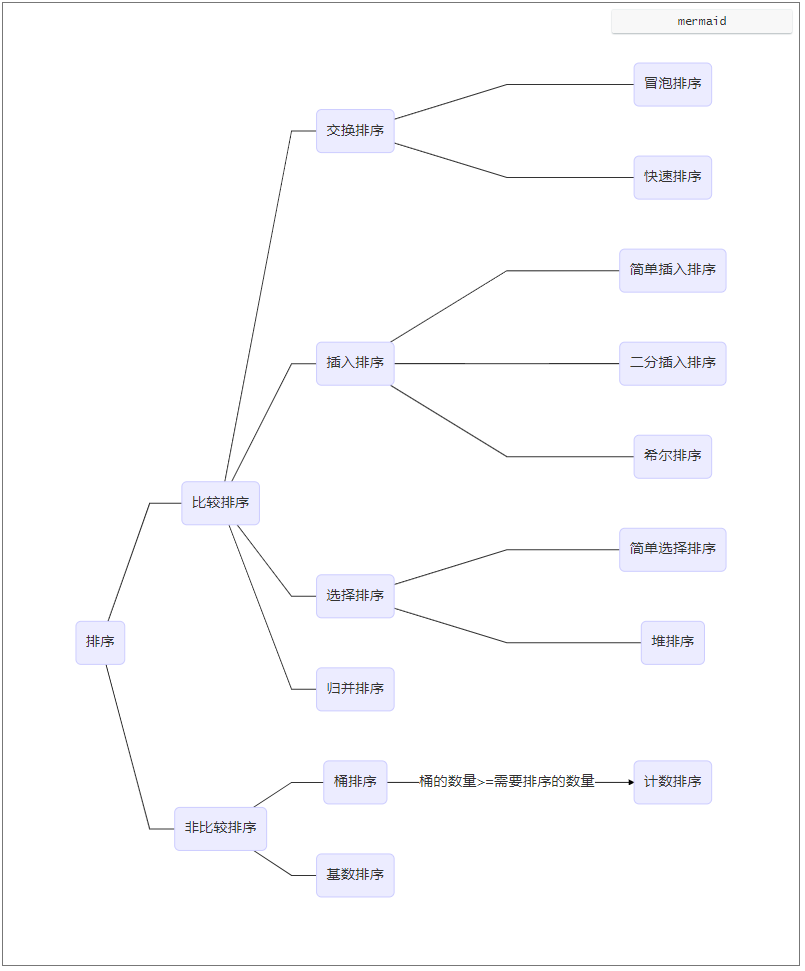
排序算法分类图
算法比较表
| 算法名称 | 最好/最差/平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | O(N) / O(N^2) / O(N^2) | O(1) | 稳定 |
| 简单选择排序 | O(N^2) / O(N^2) / O(N^2) | O(1) | 不稳定 |
| 简单插入排序 | O(N) / O(N^2) / O(N^2) | O(1) | 稳定 |
| 二分插入排序 | O(N) / O(NlogN) / O(NlogN) | O(1) | 稳定 |
| 希尔排序 | O(N) / O(N^2) / O(N^1.3) | O(1) | 不稳定 |
| 堆排序 | O(NlogN) / O(NlogN) / O(NlogN) | O(1) | 不稳定 |
| 快速排序 | O(N) / O(N^2) / O(NlogN) | O(NlogN) | 不稳定 |
| 归并排序 | O(NlogN) / O(NlogN) / O(NlogN) | O(N) | 稳定 |
| 基数排序 | O(NK) / O(NK) / O(NK) | 稳定 | |
| 计数排序 | O(N+K) / O(N+K) /O(N+K) | 稳定 | |
| 桶排序 | O(N) / O(N^2) / O(N+K) | 稳定 |
解释
基数排序中的K:待排序数组中最大值的位数
计数/桶排序中的K:待排序数组中的最大值
相关概念
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
三四句话算法讲解
冒泡排序
教科书中一定会提到的算法,采用双重循环比较的方式,每次比较将较大的数置后,每次遍历将选出一个最大的数
由于每次遍历都会比较所有需要比较的数,且需要比较N次,故平均时间复杂度为O(N^2)
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
动图展示
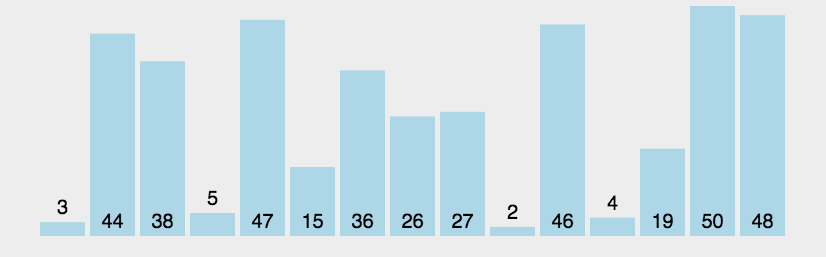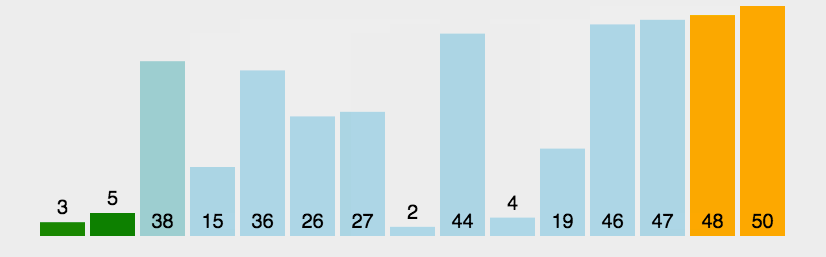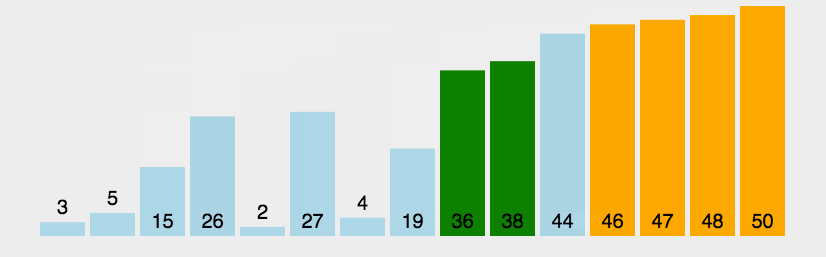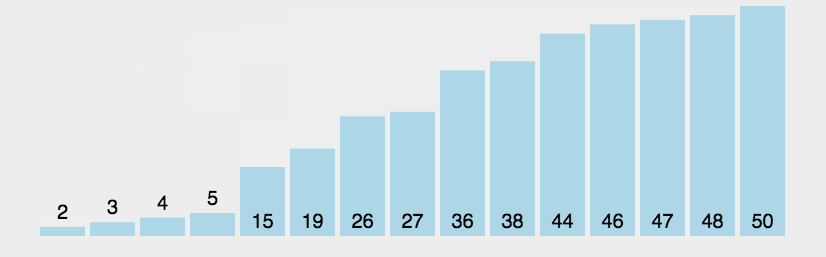
简单选择排序
采用双重循环比较的方法,每次循环比较选出一个最小值与头部交换
由于每次遍历都会比较所有需要比较的数,且需要比较N次,故平均时间复杂度为O(N^2)
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
不稳定反例数组:5 4 5 2
动图展示 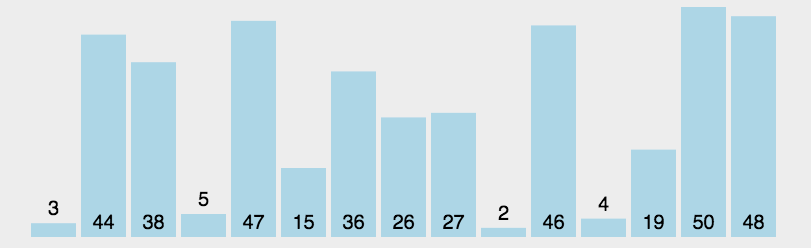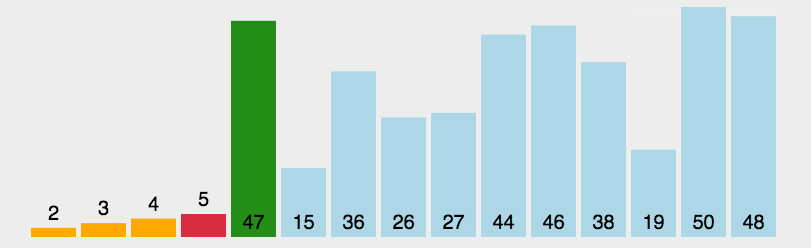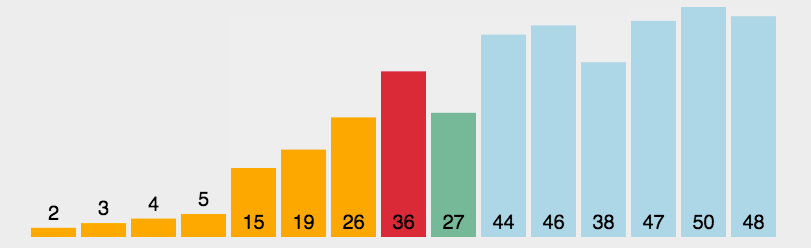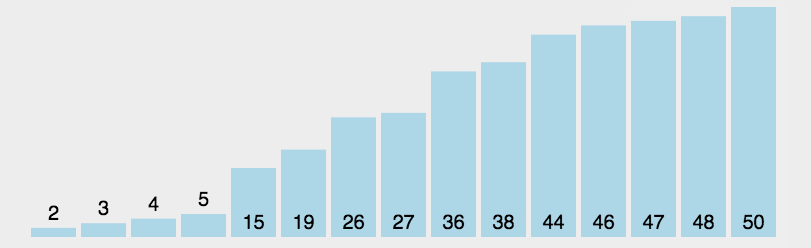
简单插入排序
假设当前排序数之前的数组有序,在之前的有序数组中顺序找出当前排序数应该插入的位置并插入
由于每次遍历都有可能比较所有有序数组中的数,且需要比较N个数,故平均时间复杂度为O(N^2)
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
动图展示 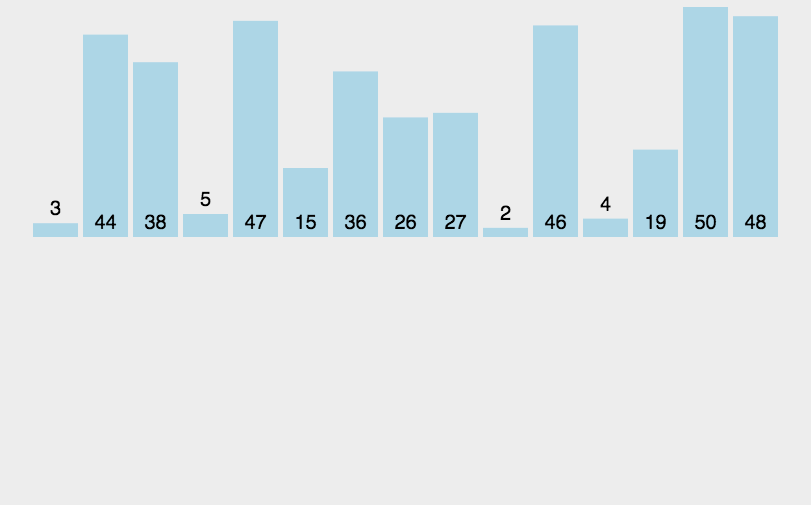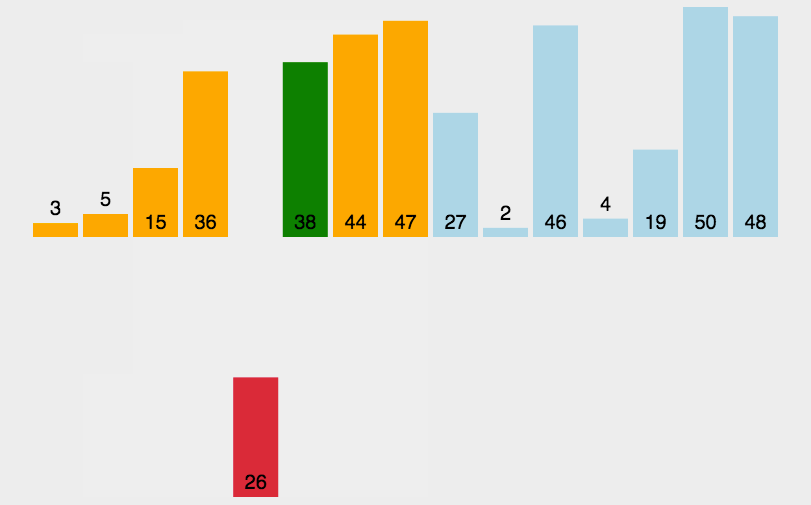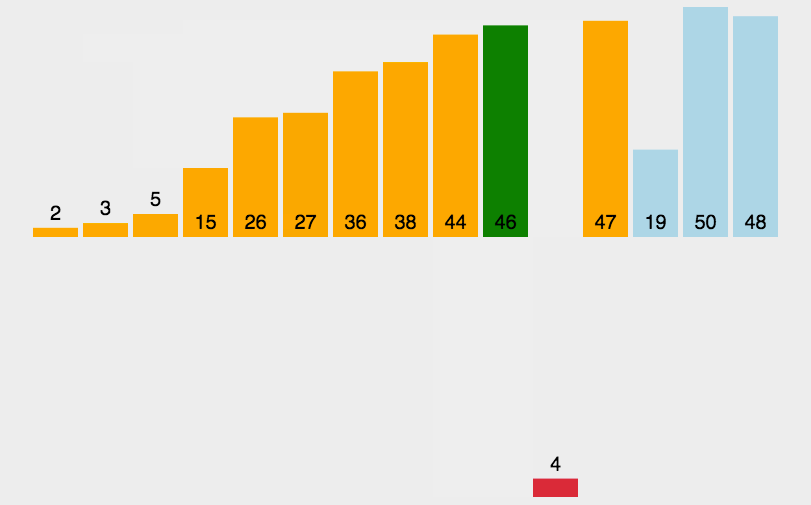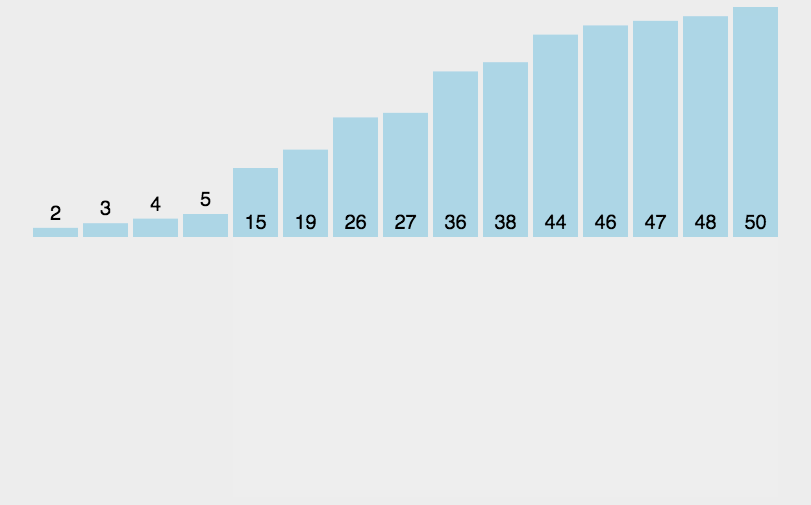
二分插入排序
假设当前排序数之前的数组有序,在之前的有序数组中使用二分算法找出当前排序树应该插入的位置并插入
二分算法查找到目标的时间复杂度为O(logN),一共需要查找N次,故平均时间复杂度为O(NlogN)
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
图片展示 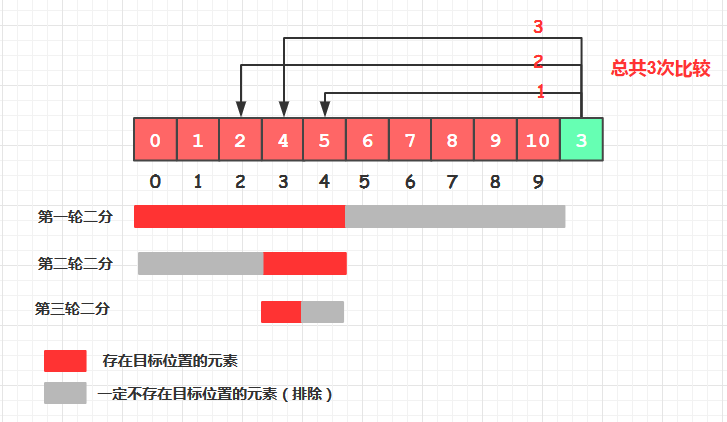
归并排序
使用分治的思想,将数组等分为两个数组,将两个数组进行归并排序,将两个有序数组合并
数组每次二等分,直到数组数量为1,经历了logN次,合并一共需要对N个数排序,故时间复杂度为O(NlogN)
合并时需要申请空间进行数组合并,故空间复杂度为O(N)
动图展示 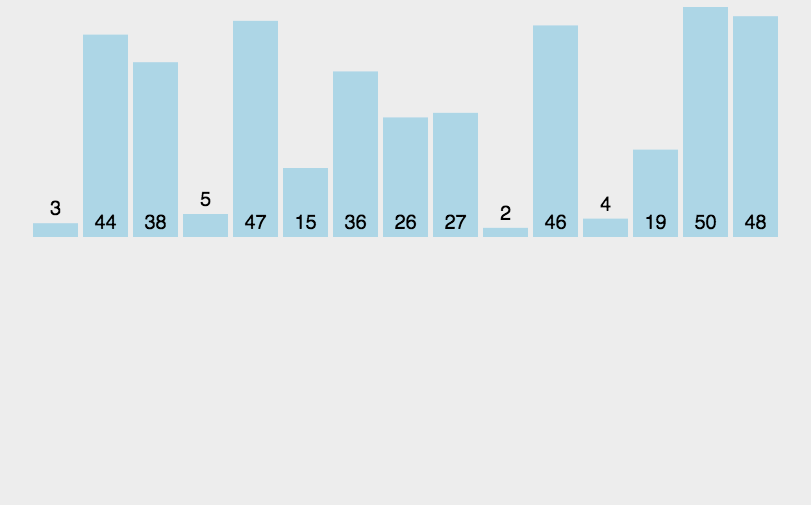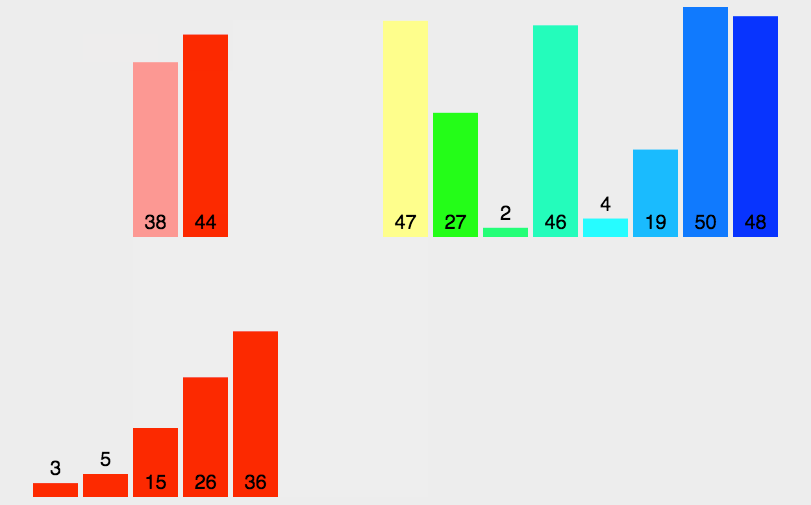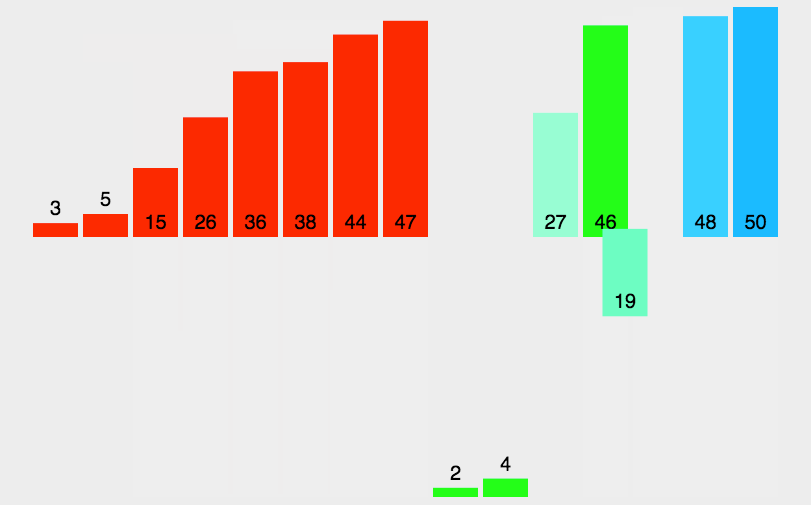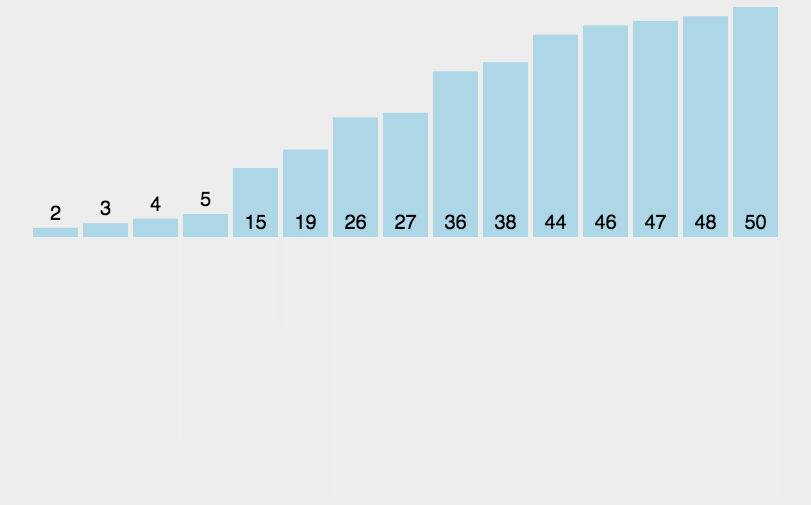
桶排序
将所有待排序数根据特定的函数公式分别放入多个桶中,对每个桶进行排序
注意:该算法的函数公式是否可以将所有数尽可能的平均分配到桶中,以及对单个桶采用的排序算法,都决定了桶排序算法总体的优劣
计数排序
桶排序的极致
- 找出最大值,初始化大小为最大值的数组作为桶
- 将每个值填入对应编号的桶中,而后顺序遍历所有桶
只需要遍历两遍待排序数组加一遍桶,故时间复杂度为O(N)
适用范围:正整数
动图展示 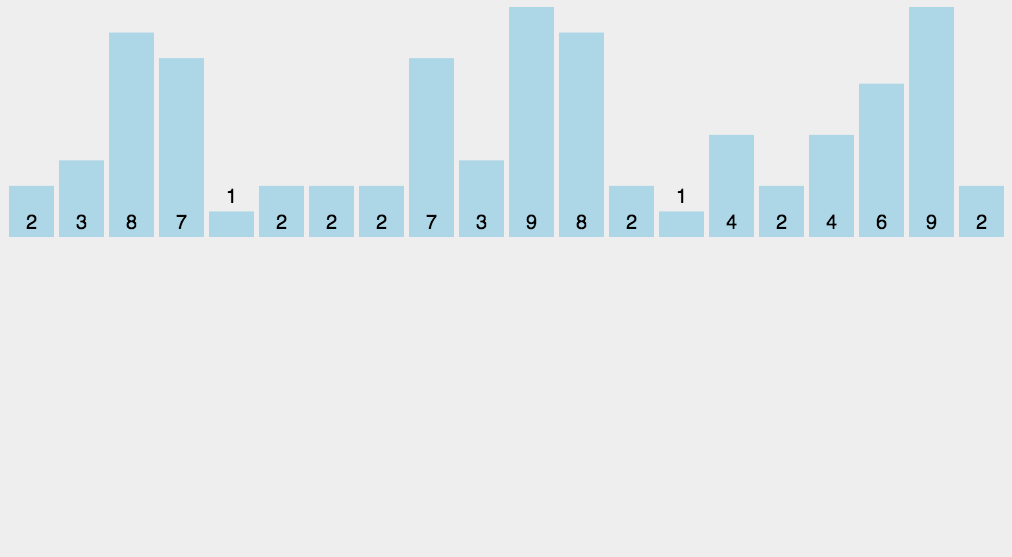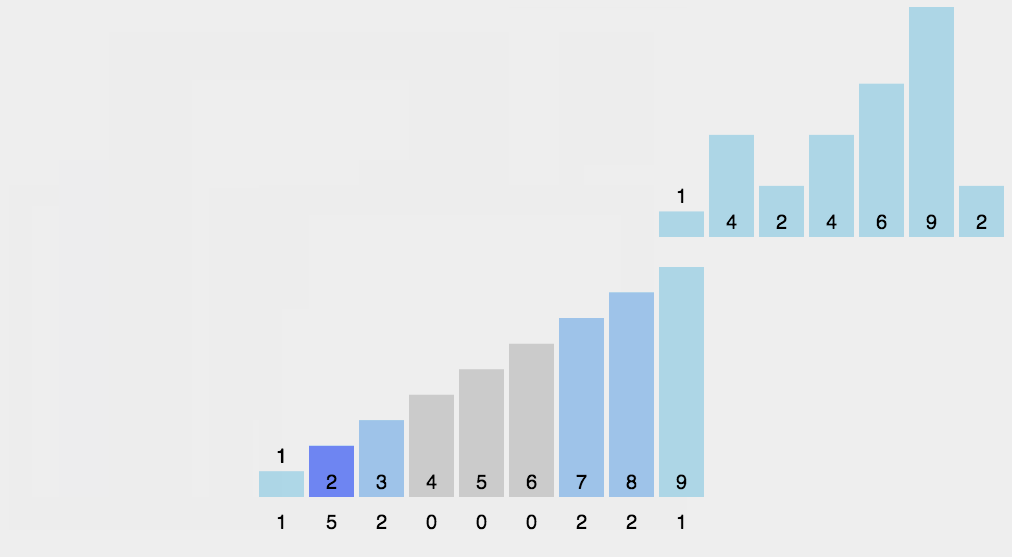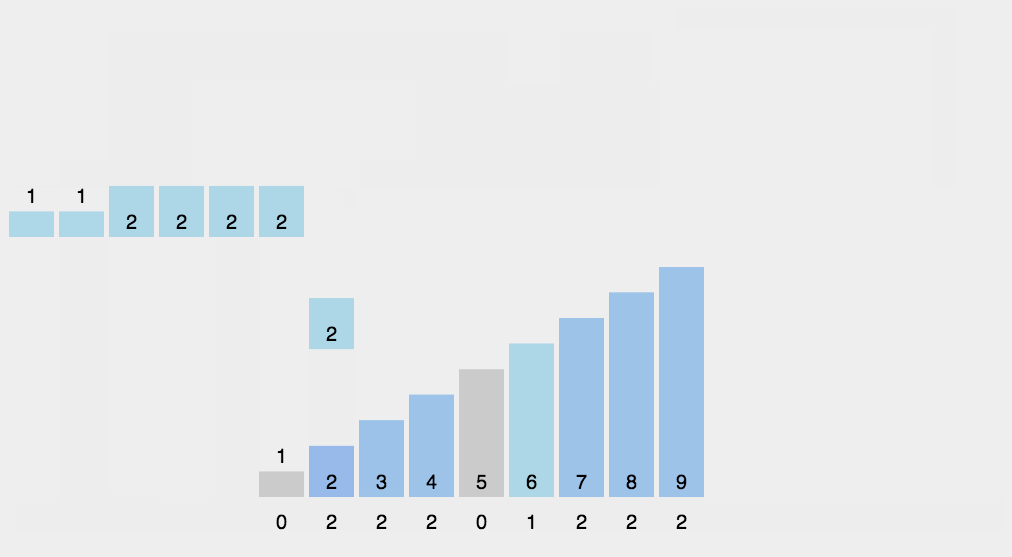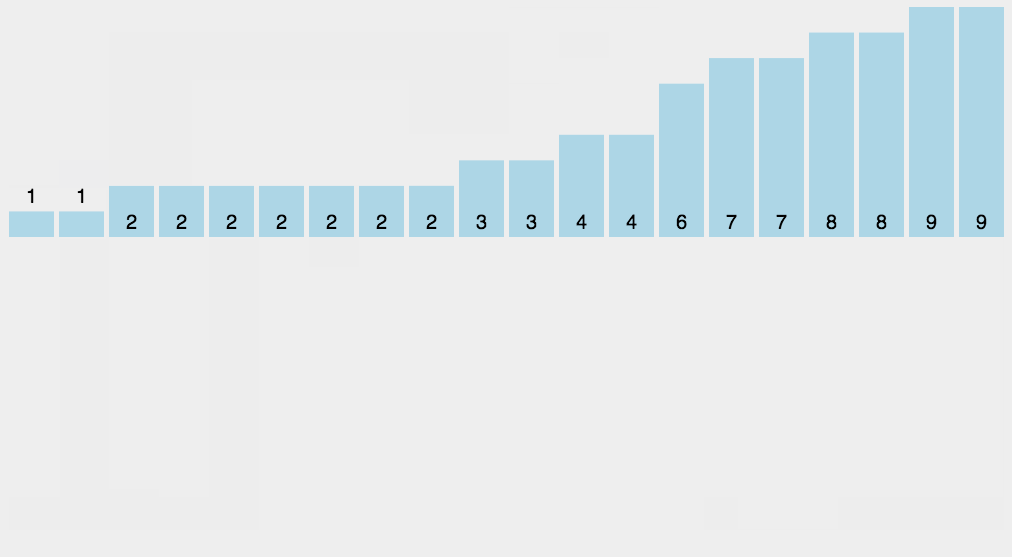
N句话算法讲解
希尔排序
又称为缩小增量排序,取整数inc作为间隔将全部元素分为inc个子序列,对每一份进行简单插入排序,而后缩小inc,直到inc=1
比较普遍的inc取数公式:
- 初始化 inc=arr.length
- inc=inc/3+1
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
不稳定反例:1 5 6 3 4 5
动图展示 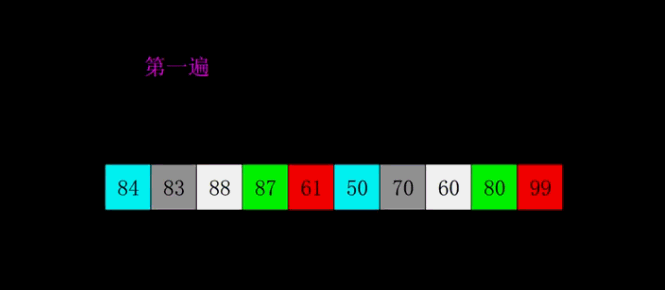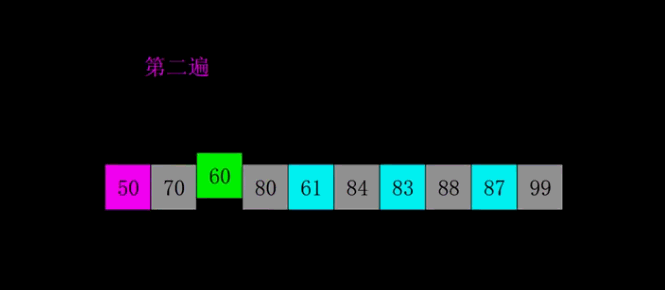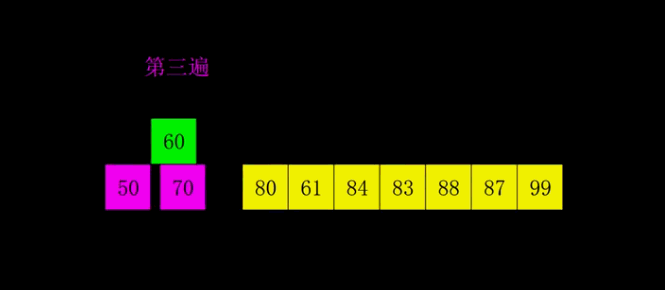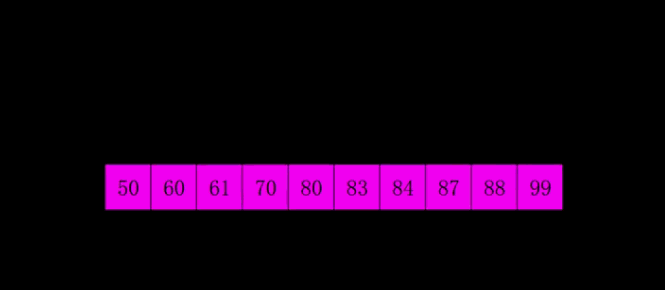
堆排序
堆:完全二叉树
大根堆:父节点 > 叶子节点
小根堆:父节点 < 叶子节点
排序过程
- 将待排序数组当成完全二叉树:父节点>叶子节点,从最后一个非叶子节点进行堆调整
- 将调整好的二叉树的根节点与最后一个节点进行交换,继续调整堆并重复该步骤
N个数形成的堆的高度为logN,需要调整N个数,故时间复杂度为O(NlogN)
由于只是待排序中的数进行比较并不需要额外的空间,故空间复杂度为O(1)
不稳定反例:9 8 7 6 5 6
动图展示 
快速排序
使用分治的思想
- 选择最左侧值为key
- 先从右边遍历找到一个小于key的值right,再从左边遍历找到一个大于key的值left
- 交换left、right
- 重复2、3步骤直到左右指针重叠,交换key值和left的值
- 对left左右两边的数组分别在进行上述步骤
注意点:选左侧值为key则要先从右侧开始找,反之要先从左侧开始找
分治的思想将数组分为两份,平均需要分logN次,一遍需要遍历N个数,故时间复杂度为O(NlogN)
不稳定反例:5 7 7 1 1
动图展示 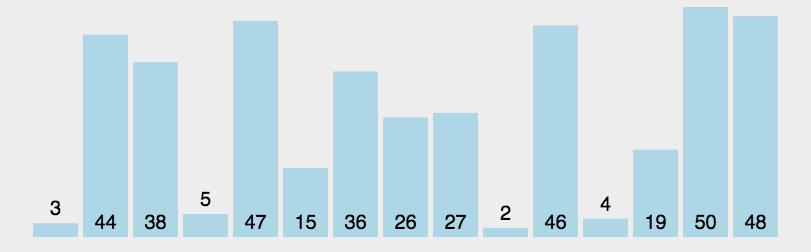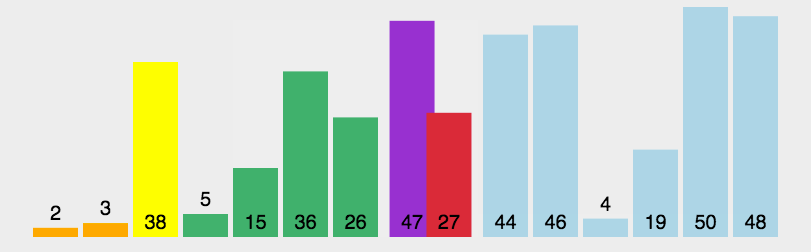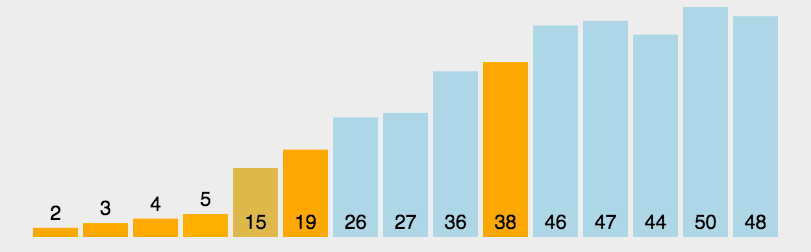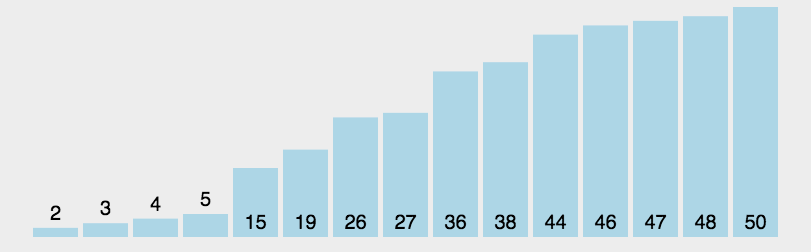
基数排序
- 找出最大值MAX,最大值的位数即为排序的次数MAXRADIX
- 准备10个桶,分别装入值为0-9的数
- 对所有数的某一位进行入桶,出桶
- 从低位到高位执行3步骤,执行MAXRADIX次
每次对所有数进行遍历,遍历次数为K次,故时间复杂度为O(NK)次
动图展示 
Java代码示例
https://github.com/VAS-QZ/keep-doing-exercises/blob/master/src/main/java/Sort.java
参考博客
https://www.cnblogs.com/onepixel/articles/7674659.html
所用到的图来自于互联网,图侵删
